공공재를 위한 최적의 펀딩 메커니즘, Quadratic Funding
공공재는 어떻게 펀딩을 해야 할까?
우리의 삶은 생각보다 많은 공공재에 의존하고 있습니다. 대교, 도서관 등과 같은 공공재는 주로 정부가 시민으로부터 걷은 세금을 기반으로 생산되고 있습니다. 또한 오픈소스 역시 공공재로서 착한 개발자들 및 소수 기부자들의 헌신 덕에 지속적으로 개발되고 있습니다.
반면 이러한 공공재는 지속적인 투자를 받기 어려울뿐만 아니라, 기부자금이 있다 하더라도 해당 자금을 어떤 공공재에 얼만큼 배분해야 하는지 결정하기 어려운 문제가 있습니다. 공공재는 일반 상품(시장에서 매매되는 재화)과는 달리 불특정 다수가 무료로 사용할 수 있는 반면, 개인마다 공공재에 대해 느끼는 가치는 다르기 때문입니다.
본 아티클에서는 공공재를 위한 최적의 펀딩 모델인 ‘Quadratic Funding(이하 QF)’에 대해 알아 보고자 합니다. QF가 공공재에 최적인 이유와 앞으로 해결해 나가야 할 문제에 대해 알아 봅시다.
1. 공공재가 갖는 문제
공공재(Public Goods)는 비배재성(non-excludable)과 비경합성(non-rivalrous)이라는 성질을 갖는 재화를 의미합니다.
비배재성(non-excludable): 비용을 지불하지 않는 잠재적 수혜자들이 재화나 서비스의 혜택을 보는 것을 배제할 수 없는 특성
비경합성(non-rivalrous): 어떤 한 사람이 먼저 재화나 서비스를 소비했다고 해서 해당 재화나 서비스의 가치 혹은 양이 감소하지 않는 특성
공공재에는 항상 아래와 같은 문제가 따라다닙니다.
무임승차 문제(free-rider problem): 공공재로 이익을 보는 사람이 대가를 지불하지 않을 때, 해당 재화나 서비스의 공급이 줄어드는 현상
공동의 결정 문제(collective decision problem): 개인이 공동 의사 결정 과정에 참여 시 미래의 성공적인 의사 결정에 부정적인 영향을 미치는 독특한 행동 패턴을 보이는 현상
무임승차와 공동의 결정 문제로 인해 공공재는 실제로 제공하는 가치 대비 적은 금액만 지원받는 경우가 다반사입니다. 이로 인해 공공재에는 ‘과잉 소비(overconsumption)’, ‘투자 부족’(under investment), 궁극적으로는 ‘자원 고갈(depletion of the resource)’이라는 문제가 초래됩니다.
공공재의 지속 가능한 생산 및 발전 가능한 구조를 위해서는, 공공제가 실제 사람들에 제공하는 가치에 비례하여 자금이 지원될 수 있도록 하는 것입니다.
이를 위해서는 공공재에 대한 선호도를 제대로 파악함으로써 기존의 ‘공동의 결정 문제’를 해소할 수 있는 모델이 필요합니다.
2. 기존 모델의 한계
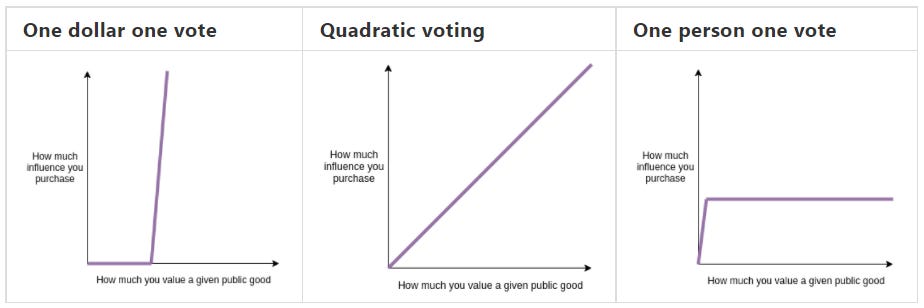
공공재의 공동의 결정 문제를 해소하기 위한 다양한 시도가 있어 왔습니다. 대표적으로는 1) 시장 경제에 따라 투표를 하거나, 2) 1인 1 투표하는 것입니다.
반면, 이 두 모델을 공공재에 적용 시 투표 결과는 잠재적 사용자의 실제 기호를 반영하지 못하는, 즉 극단적 결과를 초래하는 한계가 있습니다.
쉬운 이해를 위해 먼저 상황을 가정해 보겠습니다.
정부에서 블록체인 생태계 발전에 도움이 되는 곳에 $10,000를 매칭 펀드(matching fund)를 할 예정입니다.
매칭 펀드(matching fund): 개인 기부/투자가 이뤄진 곳에 정부, 자선단체 등으로부터 모금된 펀드를 매칭하여 지급하는 펀딩 방식
정부는 사람들의 투표 결과에 따라 $10,000를 어디에 기부할지를 결정하고자 합니다.
마침 크립토터틀은 $1,000 기부를 받게 되면 ‘2021 암호화폐 투자 전략’ 아티클을 공공에 공개할 계획이 있음에 따라 매칭 펀드를 신청하게 됩니다.
1) 시장 경제에 따른 투표
기부 방식
투표 참여를 희망하는 사람은 1투표 당 $1에 구매하여 투표를 할 수 있으며, 인당 투표 구매 수량은 제한 없습니다.
투표 시 지불된 금액은 매칭펀드 금액과 함께 투표를 받은 곳에 기부되어집니다.
1 투표 당 기부 목표 달성 가능성은 p만큼 상승되며, 이때 p는 한계 가능성(marginal probability)입니다.
따라서 투표 참여자는 k 번 투표 시 총 k*p만큼 목표액 달성 가능성을 높일 수 있습니다.
개인 참여자 행위 분석
개인이 느끼는 ‘2021 암호화폐 투자 전략’ 아티클에 대한 가치(효용)를 $V라고 할 때, 개인의 1 투표에 대한 가치는 $(p*V) 입니다.
이에 따라 투표 참여자는 아래와 같이 투표 여부를 결정합니다.
1 투표의 가치(p*V) > $1 일 경우 투표
1 투표의 가치(p*V) < $1 일 경우 투표 안 함
결과
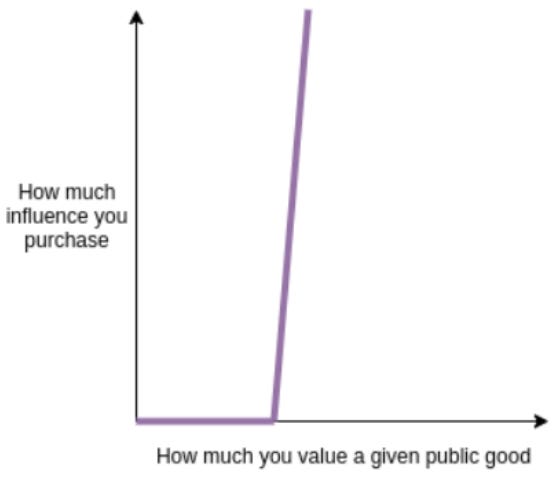
상당한 재력을 지니고 있고, 크립토터틀의 잠재 가능성을 높게 보는 사람(p*V > 1)은 원하는 만큼 크립토 터틀에 투표(기부)를 할 것입니다. 이로 인해 해당 투표 참여자의 기부에 대한 영향력은 무수히 커질 수 있습니다.
동일한 공공재에 대한 투표를 구매하는 비용은 변하지 않기(1투표 = 1달러)에 지속적으로 투표를 구매한다고 해서 부담이 크지 않습니다.
비탈릭이 2011년도 실험했을 당시, 총 기부액의 절반 이상이 한 사람으로부터 발생했다고 합니다.
반면, 크립토터틀을 잘 모르는 사람의 경우(p*V < 1)에는 투표 조차도 하지 않을 것입니다. 즉 1$ 조차도 기부를 하지 않을 것입니다. 이로 인해 해당 투표 참여자의 기부에 대한 영향력은 0입니다.
결과적으로, 시장 경제에 따른 공공재 펀딩에 대한 공동 결정 방식은 해당 공공재에 관심이 많은(혹은 부유한) 사람에게 과도한 영향력(특권)을 부여하는 한계를 가집니다.
2) 1인 1투표
기부 방식
투표 참여를 희망하는 사람은 누구든 무료로 투표를 할 수 있으며, 최대 1번의 투표만 허용됩니다.
참여자 행위 분석
모든 투표 참여자의 초기 기여 비용은 매우 낮습니다(투표만 하면 되기 때문입니다).
반면, 투표 참여자는 1번의 투표 이후 그이상으로 기부관련하여 기여하는 것은 불가능합니다.
결과
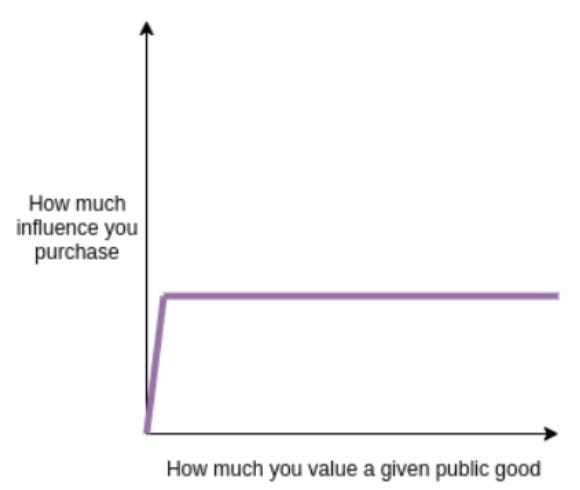
크립토터틀은 잘 모르지만 블록체인 관련 주체의 아티클이니 막연히 좋겠지하고 생각하는, 적당히 조금 관심을 가진 사람은 누구나 크립토터틀에 투표를 할 것입니다.
크립토터틀을 잘 알고 우리들의 잠재 가능성을 높게 보는 사람 역시 크립토터틀에 투표를 할 것입니다. 반면, 더 적극적으로 기부 목표액 달성에 영향을 주고 싶어도 1개의 투표권을 행사하는 것 이상으로는 불가능합니다.
결과적으로, 1인 1투표에 따른 공공재 펀딩에 대한 공동 결정 방식은 해당 공공재에 관심이 적은 사람에게 과도한 영향력(특권)을 부여하는 한계를 가집니다.
정리하면, 시장 경제에 따른 기부는 많은 관심을 갖는(또는 부유한) 사람들에게 과도한 특권을 부여하고, 1인 1투표에 따른 기부는 조금만 관심을 갖는 사람들에게 과도한 특권을 부여하는 한계가 있습니다.
즉, 두 모델 모두 잘못된 공동의 결정 문제를 초래함으로써 공공재에 대한 관심, 선호도와 무관하게 기부 금액이 결정되고 맙니다.
3. Quadratic Vote를 통한 공동의 결정 문제 해결
비탈릭 부테린은 공공재 펀딩에 대한 공동의 결정 문제를 Quadratic Vote(이하 QV)를 통해 해결할 수 있다고 합니다.
1) QV 정의
Quadratic Vote(이하 QV)는 소수 참여자가 투표권을 과도하게 행사하거나 단순히 참여자의 찬/반 의사를 표현하는 것이 아니라, 실제 참여자의 선호도에 비례하여 투표권을 행사하도록 유도하는 투표 방식입니다.
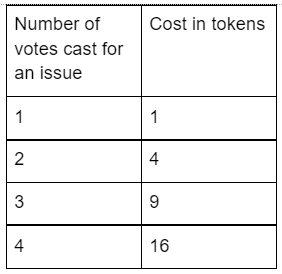
QV는 한 안건에 대해 1개 이상의 투표를 할 시, 투표 비용이 투표 수의 제곱만큼 증가하게 함으로써 해당 안건에 정말 관심이 깊은 사람만이 더 많은 비용을 들여 투표를 하도록 유인합니다.
Cost to the voter = (Number of votes)^2
2) QV의 변형 버전
Vitalic은 Quadratic Payments: A Primer에서 조금 다른 방식의 QV를 예시로 듭니다. 그 방식은 아래와 같습니다.
기부 방식
투표 참여를 희망하는 사람은 누구든 원하는 수 만큼 투표를 구매할 수 있습니다.
투표 시 지불된 금액은 매칭펀드 금액과 함께 투표를 받은 곳에 기부되어집니다.
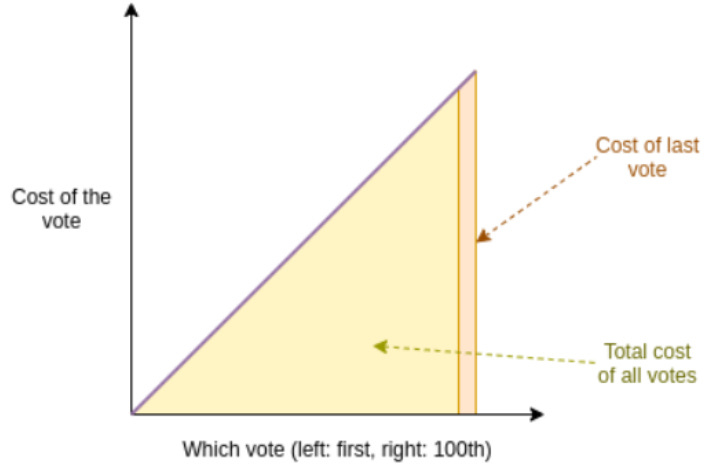
다만, 특정 아젠다에 대해 구매하는 투표의 가격은 n번째 구매 시 ‘$0.01 * n’만큼 상승합니다.
예를 들어, 첫번째로 구매한 투표의 가격은 $0.01, 두번째로 구매한 투표는 $0.02, 세번째로 구매한 투표는 $0.03..
이에따라 n번째 투표를 구매 시 총 지불한(기부한) 금액은 (n^2)/2 입니다.
참여자의 행위 분석
Alice의 크립토 터틀에서 발행하는 ‘2021 암호화폐 투자 전략’에 대한 가치는 $100입니다.
Alice는 기부 목표 달성이 1% 상승 시 $1의 가치를 얻습니다.
따라서 Alice는 기부에 1%의 영향력을 미치는데 기꺼이 $1까지 지불할 용의가 있습니다. 이에 따라 Alice는 투표 가격이 $1가 될 때까지 투표를 구매함에 따라 총 100개의 투표를 구매합니다.
Vitalic은 개인이 공공재에 대해 느끼는 가치가 one unit of influence에 지불하고자 하는 금액을 결정하는데 영향을 미친다고 강조하였습니다.
이때 one unit of influence는 상황에 따라 다르게 정의될 수 있습니다. 예를 들어, 앞선 시장 기반 투표에서는 1 투표가 공공재에 미치는 영향이 one unit of influence였다면, 본 QV 예시에서는 공공재 펀딩 1% 증대에 대한 영향이 one unit of influence입니다.
Bob의 크립토 터틀에서 발행하는 ‘2021 암호화폐 투자 전략’에 대한 가치는 $50입니다.
Bob은 기부 목표 달성이 1% 상승 시 $0.5의 가치를 얻습니다.
따라서 Bob은 기부에 1%의 영향력을 미치는데 기꺼이$0.5까지 지불할 용의가 있습니다. 이에 따라 Bob은 투표 가격이 $0.5가 될 때까지 투표를 구매함에 따라 총 50개의 투표를 구매합니다.
결과
Alice의 ‘2021 암호화폐 투자 전략’ 아티클에 대한 가치가 Bob 대비 2배인 만큼 Alice가 구매한 투표는 Bob의 2배가 됩니다.
이에 따라 다른 모델 대비 QV 방식은 실제 투표 참여자의 공공재에 대한 관심, 선호도에 비례한 투표 결과를 가져올 수 있습니다.
4. QF를 통한 공공재 별 펀딩 금액 결정
QV는 보다 투표 참가자들의 의사가 잘 반영된 결정을 내릴 수 있도록 하지만, 여전히 공공재에 ‘얼만큼’의 금액이 기부되어야 하는지는 결정하지 못한다는 한계가 있습니다.
즉, 위 가정된 상황 하에 QV를 통해 어떤 공공재가 실제로 더 인기있는지 판단할 수 있더라도, 투표를 받은 공공재가 복수개일 경우 정부의 펀드를 각 공공재에 얼만큼씩 배분하는게 좋은지 결정하는 것은 여전히 어려운 문제입니다.
이에 대한 해결책으로 Vitalik buterin, Zhitzig 그리고 Glenweyl은 Quadratic Funding(이하 QF) 모델을 개발하였습니다.
QF는 ‘기부에 참여한 사람 수’를 기반으로 공공재의 우선순위를 결정함으로써 매칭 펀드의 효과를 극대화할 수 있게 하는 모델입니다.
앞으로 QF에 대해 보다 자세히 알아보겠습니다.
1) Quadratic Funding 원리
QF가 이뤄지는 프로세스는 아래와 같이 매우 간단합니다.
개인은 공공재(eg. 오픈소스 프로젝트) 크라우드 펀딩에 참여합니다.
이러한 개인에 의한 기부를 토대로 정부, 그랜트 프로그램, 개인 자선가가 기부한 펀드가 각 공공재에 매칭됩니다.
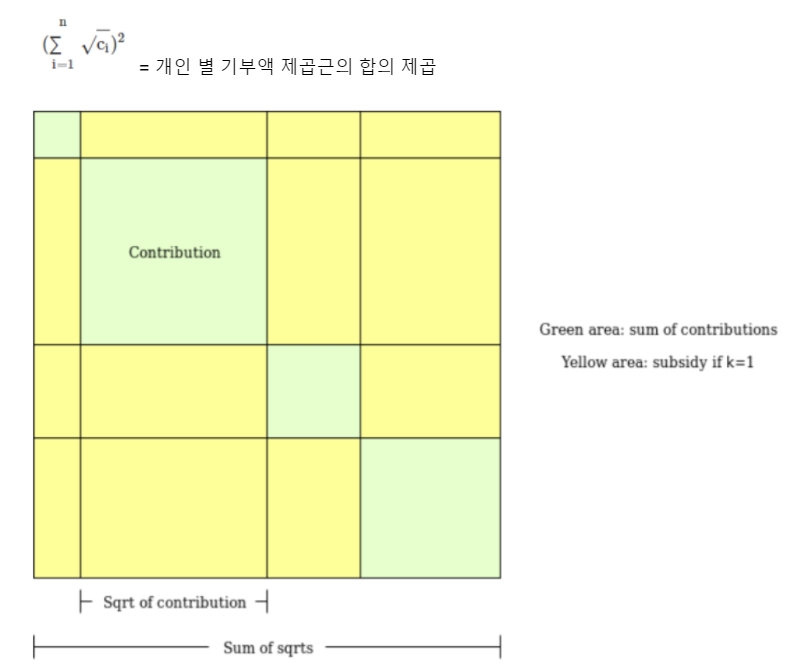
위와 같은 절차를 통해 공공재가 획득하게 되는 총 기부액은 아래와 같습니다.
즉, 공공재가 매칭 펀드로부터 배분받은 금액은 ‘개인 별 기부액의 제곱근의 합의 제곱’에서 ‘개인이 기부한 금액’을 제외한 것입니다(eg. 2명이 각각 $1씩 A 공공재에 기부할 시, A공공재가 총 획득한 금액은 $4(2^2)이고, 이중 $2는 매칭 펀드로부터 배분받음). 따라서 위 그림과 같이 개인이 기부한 것 보다 매칭 펀드로부터 배분받은 금액이 더 큰 경우도 있습니다. 반면, 매칭 펀드 풀이 크지 않을 경우에는 ‘개인 별 기부액의 합의 제곱’에 비례하여 배분하면 됩니다.
보다 쉬운 이해를 위해 구체적인 예를 들어 보겠습니다. (혹은 다음 QF 시률레이션 툴을 이용해 볼 수 있습니다)
위 가정과 같이 현재 정부로부터 확보된 $10,000 펀드가 있습니다.
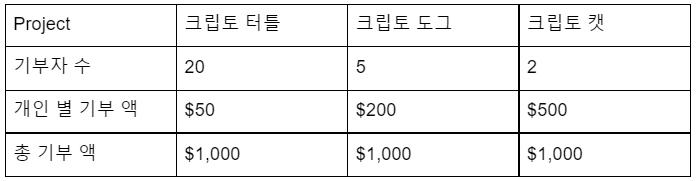
아래와 같이 크립토터틀을 포함하여 3개의 프로젝트가 크라우드 펀딩을 받았습니다.
각 프로젝트 별 기부금의 제곱 값은 아래와 같습니다.
크립토 터틀: (20*(루트50))^2 = 400*50 =20,000
크립토 도그: (5*(루트200))^2 = 25*200 =5,000
크립토 캣: (2*(루트500))^2 = 4*500 =2,000
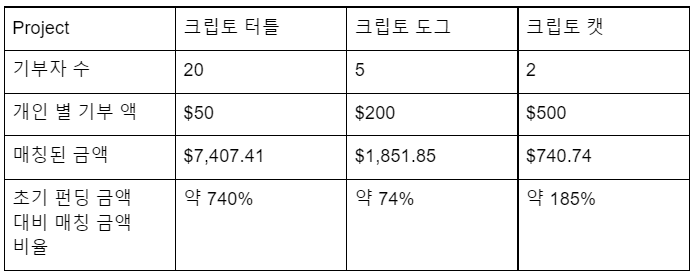
각 프로젝트 별 매칭 금액은 비율에 따라 아래이 결정됩니다.
크립토 터틀: (20/(2+5+20)) * $10,000 = $7,407.41
크립토 도그: (5/27) * $10,000 = $1,851.85
크립토 캣: (2/27) * $10,000 = $740.74
정리하면, 동일 금액을 기부받더라도 더 많은 유저에게 기부받은 크립토 터틀이 가장 많은 펀드 금액을 매칭받게 됩니다.
2) Quadratic Funding의 장점
QF의 대표적인 장점은 2가지가 있습니다.
실제 여러 사람에 의해 사용될 공공제에 보다 많은 펀딩이 이뤄지면서 공유지의 비극 문제(the tragedy of the commons problem)를 해결할 수 있습니다.
소액이더라도 여러 사람으로부터 기부를 받은 공공재는 그만큼 많은 사람들이 사용하고자 하는 공공재라는 뜻입니다. 이에 따라 QF는 기부액이 아닌 ‘기부자 수’에 보다 초점을 두고 공공 펀드를 매칭해 줍니다.
소액 기부자에게 기부 동참 인센티브를 제공합니다.
QF는 기부에 동참하는 사람 수가 많을 수록 매칭되는 금액이 증가하기에 소액 기부자이더라도 해당 공공재에 미치는 영향력은 상당할 수 있습니다.
또한 앞선 시장 기반 투표의 경우 구매 투표 수(기부액)에 따라 공공재 기부에 대한 영향력이 리니어하게 상승하는 반면, QF에서는 기부액을 늘리더라도 공공재에 대한 한계 영향력(marginal influence)은 점점 감소합니다.
3) QF 활용 사례; Gitcoin
깃코인은 오픈소스 소프트웨어 크라우드펀딩 플랫폼으로, QF를 기반으로 다양한 오픈소스 프로젝트에 대한 펀딩을 지원하고 있습니다.
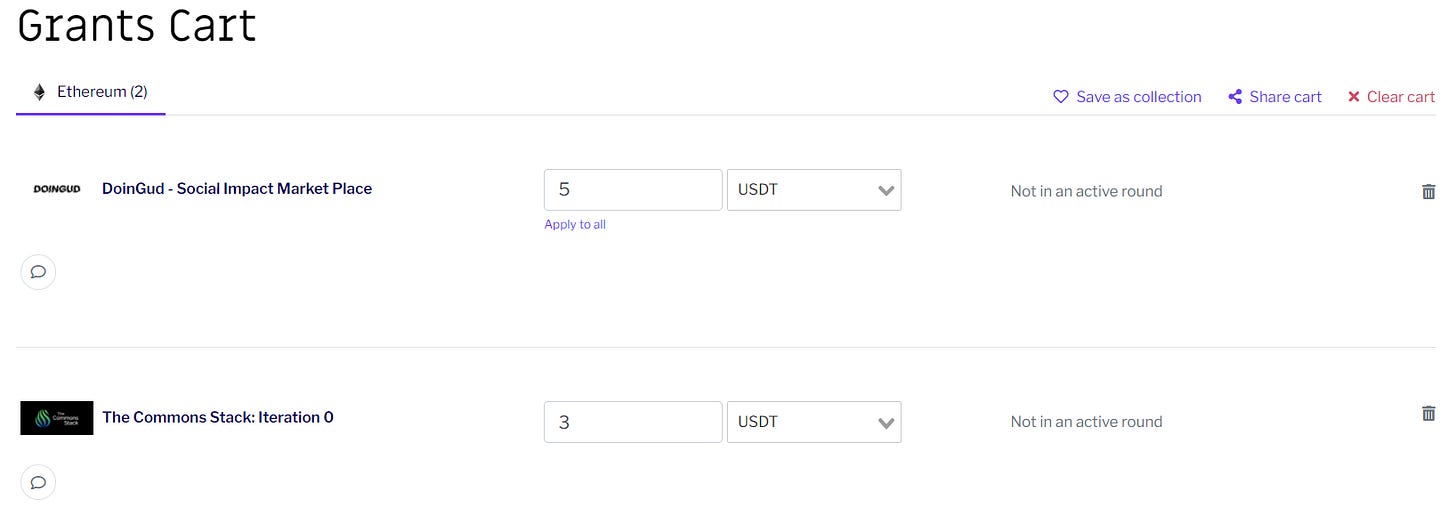
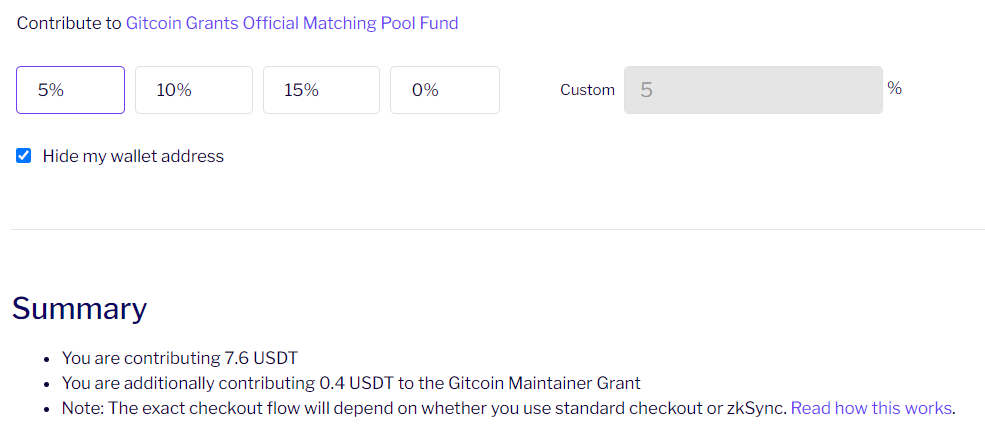
깃코인을 통해 QF에 참여하고 싶다면 ‘깃코인 Grant’ 페이지로 가서 기부를 희망하는 프로젝트들을 카트에 담고 프로젝트 별 기부할 액수를 입력하면 됩니다.
이 중 일부는 매칭펀드를 위한 풀에 기부될 수 있습니다(강제이지만..).
기부를 완료하면 아래와 같은 팝업이 뜹니다.
깃코인은 벌써 QF를 7라운드까지 마무리하였으며, 현재까지 총 약 $2M이 QF 프로젝트를 통해 배분되었다고 합니다(참고로 깃코인은 현재까지 약 $28M 상당의 오픈소스 프로젝트에 대한 기부를 달성하였습니다).
깃코인이 진행하는 QF에 대한 자세한 사항은 다음 링크를 통해 확인 가능합니다.
5. 마무리 지으며..
QF는 다른 기부 모델 대비 갖는 명확한 장점에도 불구하고, 아래와 같은 한계가 있습니다.
시빌 공격에 대한 취약성
여전히 자선가에 대한 높은 의존도
깃코인 및 QF를 개발한 Vitalic 등은 QF의 한계를 극복하기 위해 아래와 같이 지속적으로 QF모델을 보완해 가고 있습니다.
동일한 양의 보조금을 동일한 공공재에 기부하는 pair가 있을 시, 해당 pair의 기부가 증가할 수록 pair의 기부에 대해 매칭되는 금액은 감소
기부자 신분 증명
본 아티클을 작성하면서, 공감이 갔던 부분도 있고 가지 않았던 부분도 있었습니다.
예를 들어, 우리가 기부를 결정할 때 정말로 one unit of influence를 고려해서 결정하는가가 의문이었습니다. 또, QF가 적합한 공공재에 대한 funding을 유도할 수 있는 반면, 공공재에 대한 funding 자체를 극대화하지는 못한다는 인상을 받았습니다.
반면 QF는 공공재를 단순히 감정적(인자함, 동정심 등)으로 접근하기 보다는, 명확한 로직과 체계적인 시스템적으로 접근한다는 점이 좋았습니다. 이처럼 공공재를 지속가능하게 활성화하기 위한 노력은 계속되었으면 하고, 이런 펀딩 모델들을 앞으로 계속 더 찾아 보고자 합니다 :)
이미지 출처
Quadratic Payments: A Primer: https://vitalik.ca/general/2019/12/07/quadratic.html
참고 자료
gitcoin; wtf QF: https://wtfisqf.com/?grant=100,100,100,100&grant=1,10,100,5000&grant=200000&match=1000
Quadratic Payments: A Primer: https://vitalik.ca/general/2019/12/07/quadratic.html
How Can $1 Turn Into $27? Quadratic Funding Explained: https://finematics.medium.com/how-can-1-turn-into-27-quadratic-funding-explained-34591e2b93cc
Gitcoin Grants Quadratic Funding Implementation: https://github.com/gitcoinco/quadratic-funding
Quadratic Funding — A Better Way to Fund Public Goods: https://blog.woodstockfund.com/2021/05/20/quadratic-funding-a-better-way-to-fund-public-goods/
How to Attack and Defend Quadratic Funding: https://gitcoin.co/blog/how-to-attack-and-defend-quadratic-funding/

너무 자세한 소개 감사합니다 : )